Henk Tolsma
Trillingen van snellopende machine-onderdelen, fladderende vliegtuigvleugels, beheersing van chemische processen, spanningen in gewapend beton, temperatuurbestendigheid van materialen. Er is wiskunde nodig om daaraan te rekenen en te voorkomen dat er problemen ontstaan.
Technische wiskunde
Wiskunde is de taal van de techniek en haar toepassingen. Wiskundige modellen spelen een grote rol in fysische en technische verschijnselen. Wiskunde wordt toegepast op technische en fundamentele problemen. Wiskundig redeneren staat centraal bij modelleren en optimalisatie, in numerieke methoden, differentiaalvergelijkingen, analyse en stochastiek.
Wiskunde is een universele taal, die overal ter wereld hetzelfde is. ‘De natuurwetten zijn geschreven in de taal van de wiskunde’, schreef Galileo Galilei (1564-1642). Wiskunde stond centraal in de film A Beautiful Mind, en in Dan Browns’ boek De Da Vinci Code.
Voor veel studenten is wiskunde echter een abstract, soms afschrikwekkend vak. Tijdens mijn technische opleiding (mts/hts) heb ik een stevig pakket wiskunde gehad: algebra, meetkunde, geniometrie, integreren en differentiëren. Een enkel jaar ging dat goed en vond ik het leuk, maar de meeste jaren niet. Dat hing vooral af van de leraren: konden zij goed en begrijpelijk uitleggen? Een enkeling kon dat, de meesten niet. In mijn werk als technisch journalist heb ik met die kennis nooit weer iets gedaan.
De wiskunde heeft inmiddels een zo abstracte staat bereikt dat zelfs de beste wiskundigen veel problemen niet meer begrijpen. Dan is het een hele uitdaging om dergelijke informatie over te brengen op het algemene publiek. Wiskundigen kunnen theorieën ontwikkelen en berekeningen uitvoeren, maar ze kunnen deze ideeën niet altijd volledig begrijpen, verklaren of overbrengen.
Om technische wiskunde te beoefenen moet je beschikken over een flinke dosis motivatie, een groot doorzettingsvermogen en abstract denkvermogen. Eén van de vakken is lineaire algebra: het rekenen met matrices en vectoren, waarmee je verschillende typen problemen met meerdere vergelijkingen kunt vereenvoudigen en oplossen of benaderen. Met wiskundige analyse leer je bijvoorbeeld differentiëren en integreren op formele wiskundige wijze, niet alleen bij functies met één variabele maar ook in hogere dimensies.
Toegepaste wiskunde
Bij de meer toegepaste vakken kun je denken aan modelleren: hoe kun je wiskunde toepassen op problemen uit de werkelijkheid. Je beschrijft de werkelijkheid in een wiskundig model en probeert de problemen op te lossen. Bijvoorbeeld: hoe dicht achter elkaar kunnen vliegtuigen op een luchthaven landen?
Ben je daar goed in en vind je het nog steeds interessant en/of leuk dan kun je je wagen aan vakken zoals ‘computational science and engineering, discrete mathematics and optimization, mathematics of data science, mathematics of quantum technology and computation, en stochastics’, aldus de website van de bacheloropleiding Technische Wiskunde van de Rijksuniversiteit Groningen.
Complexe takken van de wiskunde zoals de chaostheorie zijn terug te vinden in beelden van opkringelende sigarenrook of in het wolkje melk in koffie.
Waar kun je met wiskunde aan de slag? Bij ingenieursbureaus, een onderzoeksafdeling van (grote) bedrijven, aan universiteiten. Je kunt dan denken aan functies zoals consultant, docent, onderzoeker, risico-analist of data-analist.
Ingenieurspraktijk
Maar wat doen ingenieurs daadwerkelijk met wiskunde in de dagelijkse praktijk? Bij Technisch Weekblad, één van de technische bladen waar ik heb gewerkt, hielden we – alweer ruim tien jaar geleden – een enquête onder een dertigtal ingenieurs waarmee de redactie contacten had en werd hen gevraagd wat ze met hun wiskundige kennis hadden gedaan. Minder dan de helft van hen – werkzaam in onderzoeks-, ontwikkelings- en ontwerpfuncties – maakte daar inderdaad gebruik van. En ruim de helft had die kennis niet meer nodig gehad. Dat waren vooral ingenieurs in beleids-, marketing- en uitvoerende functies. Een deel van hen gaf echter aan de wiskundelessen wel op prijs te hebben gesteld.
Ontwikkelingen in de wiskunde
Wiskunde is ooit, tienduizenden jaren geleden, begonnen met tellen. Daarop volgde rekenen. En veel later algebra, waarbij getallen zijn vervangen door letters. In de moderne tijd volgde numerieke wiskunde, de rekenkunde van de digitale techniek, waarbij alleen met nullen en enen wordt gewerkt.
In onze tijd is wiskunde alomtegenwoordig. Het speelt een belangrijke rol in de techniek, natuurkunde, scheikunde en economie. Wiskunde helpt om supersonische vliegtuigen, ruimteschepen en achtbanen te bouwen.
Pythagoras, Gauss, Euler, Newton, Fermat, het zijn slechts enkele namen van grote geleerden die fundamenten hebben gelegd voor de wiskunde. Als we ons verder beperken tot vooraanstaande wiskundigen die de aanzet hebben gegeven tot technische ontwikkelingen, met name de informatietechniek, dan horen daar zeker Charles Babbage (1792-1871) en George Boole (1815-1864) bij.
Babbage is beroemd vanwege zijn ontwerp van een handmatig aangedreven mechanische rekenmachine, een vroege voorloper van de computer. Boole ontwikkelde een simpele algebra met twee grootheden, 0 en 1, en drie bewerkingen: en, of en niet. Zij, en ook Alan Turing (1912-1954), John von Neumann (1903-1957) en Claude Shannon (1916-2001) hebben de basis gelegd voor de huidige informatica-revolutie met onder andere neurale netwerken.
Magie van wiskunde
Wiskundigen geven graag hoog op van het verheven, bijna goddelijke karakter van hun discipline. De wiskunde kent inderdaad prachtige oplossingen en verschijnselen. Neem, als voorbeeld, het magisch vierkant van kunstenaar Albrecht Dürer uit 1514.
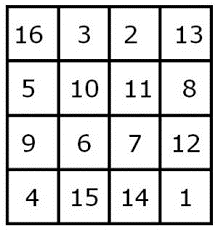
Horizontaal en verticaal is de som van de getallen in elke rij en kolom 34, evenals in de diagonalen, de hoekgetallen en het middelste vierkant.
Dit is overigens voor het huidige computertijdperk een zeer eenvoudig voorbeeld van een magisch vierkant. Inmiddels zijn er veel complexere varianten ontwikkeld, in vier dimensionale hyperkubussen die in elke mogelijke richting een magische som hebben.
Zie ook de rij van Fibonacci (1170-1250), waarvan de eerste getallen zijn: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 81 ….. Elk getal is de som van de twee voorgaande. Die reeks komt vaak voor in de natuur, zoals in blaadjes van de lelie, boterbloem en margriet. Of de Möbiusband, een prachtig gedraaid voorwerp met slechts één vlak, een ontdekking van de Duitse wiskundige August Möbius (1790-1868).


Dit is een cardioïde. Deze ontstaat door het volgen van een punt op een cirkel die om een andere cirkel met dezelfde straal draait. De naam cardioïde is afgeleid van het Griekse woord voor hart. Dit principe heeft ook een technische toepassing. Een cardioïde of unidirectionele microfoon is zeer gevoelig van voren en beperkt van achteren. Hierdoor registreert deze voornamelijk de geluidsbron en niet of nauwelijks geluiden van achteren of reflecties via muren.
Het antwoord op het nut van wiskunde voor de dagelijkse ingenieurspraktijk is deels gegeven. Maar er is nog iets anders. Wiskunde is een taal die je leert logisch te denken. Daar heb je ook profijt van ook als je niets meer rechtstreeks met dat vak doet. Met Grieks en Latijn op het gymnasium doe je ook nooit meer iets, maar je krijgt er wel een beter taalgevoel van. Veel woorden uit de moderne talen zijn afgeleid van die oude talen. En je leer ter beter door puzzelen!
Bronnen: de websites van de afdelingen technische wiskunde van de TU Delft en van de Universiteit van Groningen. En de boeken: Het wiskunde boek, 50 inzichten wiskunde, Wiskunde zien & begrijpen, Algebra.




